| LESSON 4 | Candidates | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This is a term used by other web pages used to represent the PENCILed numbers that are POSSIBLE in the squares. It is said that puzzles that have less than 26 of the 81 squares (ie 3x3x 3 rows x 3 columns) then what we have learned in Lessons 1-3 will stop producing results quickly. So we must start analyzing our pencil marks or "candidates" to start solving the next batch of numbers. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a. Numbers For The Squares |
Here we are looking for possible numbers which will fit into the remaining squares. We look at block 1 first. We see there are 4 empty squares. Lets fill in pencil what is ALLOWED to be in those squares. We are trying to figure out what numbers could fit into those squares. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
We use the row elimination technique to draw the lines across and we pencil in what the possiblities are. I have shown them in red.
So at this point we look carefully through our numbers. We looking for numbers which are by themselves or they only appear in one stop of the cells. So ws see "9" is all by its lonesome because the 5,6,7,8 are all not allowed becuase you see then on the right of that row. What does that leave? The one and only number left for that square, the "9"! PEN it in, and eliminate the other 9's from the cells.
So now this thing looks like this. We also spot that there is only one place for the "8". Since there are no 8's on the top row, it can only appear in the bottom square. Again, this is another situation were ONLY one candidate is left for that square in the block. Again, PEN the 8 in.
There we go, we went down from 5 unknowns down to 3. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b. Squares For the Numbers
|
Now, we look down the centre row, and we have numbers 1,2,5,6,7,8,9 thus we are missing a "4" and a "3". So we pencil in where the 4 and 3 is allowed to go. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
So this method is like 4a, but now you know you only have a 4 and 3 left to place. You try to figure out which of the squares it is allowed to be in. Notice that there is a 4 in the lower block. So your pencilling will give you this.
So according the process of elimination and the candidate rule you just learned in 4a, the 3 can ONLY be in the right block. So you can now PEN that 3 in and update the other squares by removing the 3's with your eraser.
Again, that only leaves the pencil 4 on the right hand side, so you can now PEN that 4 in since that is the only digit from 1-9 left that is left to fill in.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
c. Pairs
|
Ok, this one is a bit tough to grasp the concept but here I go. It is said that if a pair of 2 squares in a (row/column/block) has only 2 possible candidates, then those candidates MUST belong in those 2 squares and thus CANNOT appear anywhere else in that (row/column/block). You will remember that I told you to circle the only two candidates in the previous lesson, this is why you do it. Wow, sounds kinda complicated. So I will show it by examples. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
i) Rows
|
Ok, I will start with a ROW example.
You will note in this example, block 1 has only 2 squares left.
Ok, we now have pencilled in the possible candidiates. Now it is important to identify some very subtle properties of this "pairs rule".
So, lets use our eraser and update the pencil marks for that row by eliminating all the 6's and 7's from that row only.
Now if you are lucky, like in this example, the list of candidates of some of the other squares along that row will shrink. Shrink so much that it becomes obvious by the candidates rule that we covered earlier in part 4a of this chapter. We see that the "4" and the "3" by this process of elimination to be the only possible along this row in block 2. So we can PEN the "4" and "3" in and update our pencil marks.
Ok, I know I can keep doing the chain reactions, like the 3 in block 3 but in this example, I only wanted to illustrate how paired rows work. When you solve your sudoku puzzle, remember to check your chain reactions and do your updates to your pencil marks. Sometimes it just takes one of these special tricks to "unlock" that nasty number that is preventing the puzzle to being an easy one. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ii) Columns | Ok, columns works the same way that a row pair does, but it is applied to a column. I will quickly show it here for completeness sake. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ok, we first pencil in the possible candidates for column 1.
Ok, we can see that we have 2 squares with 2 & 3 paired possibility. We also have 2 squares with a possibility of 1,2,3,6 in them. Now let us review the properties of this "pairs rule" again.
So, lets use our eraser and update the pencil marks for that row by eliminating all the 2's and 3's from that column only.
Alas we uncover another pair for this rule 1 and 6. With this example, no more chain reactions can be done at this time. But lets say a it causes the pair rule for a block example. I will show this next. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
iii) Block
|
So, the last way a pair interacts is in a block. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lets pencil in all of block 7. As shown in the previous example, the 2's and 3's could be eliminated from the first column using the pairs rule for the column. So you can remove the 2's and 3's from that column ONLY. Beware of the temptation of removing the 2's and 3's from the block because you can't do that.
So now, we have our example of a block pair.
Now let us review the properties of this "pairs rule" again.
So, lets use our eraser and update the pencil marks for that block by eliminating all the 1's and 6's from that block only.
Like so. Again, this causes the chain reaction of the last candidate rule for the square with the 8 in the centre. Note is the only place for the 8 to appear in this block so we can PEN that one in.
One could say we have revealed another block pair rule with the 2 and the 3, but we have already by elimination gotten rid of all the other 2's and 3's from this block so this is as simplified as this block will get. We will have to stop working on this block until we get some other clues from other parts of the puzzle. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
5. Triples
|
This is actually an extension of the Pairs rule and in theory can be even extrapolated to a quadruples rule. It basically states that if we have ONLY 3 squares of a row,column or block, which share ONLY 3 numbers (and their subsets) between them, then those 3 numbers CANNOT be in any of the other 6 squares of the row, column or block. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
i. Full Set
|
Ok, lets take a row that looks like this.
Now finding triples in this mess of crap is not always easy but this one is. You can quickly see that 239 is three numbers that show up in 3 squares only. Ok, lets review why 239 is a valid triple.
Now, lets pull out our eraser and wipe out the 2's, 3's, and 9's from the other squares.
Well, lo and behold, we have eliminated enough candidates out of some of the other squares to logically fill them in. The 4 is now the only candidate left in square 8, and once you PEN that one in and update, the 1 is the only candidate left in square 5. So your row will look like this.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ii. Subset
|
The triple rule also works with subsets of the 3 candidates. They are much harder to spot but they still work. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ok, I have modified the example from above a little just to show it still works. The triple combo is still 239, but you notice now one of the three squares only has 39. This combo still works. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
iii. Minimum Subset
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Even if the row looks like this, the 239 combo still works. While you are looking at 39 as a pair combo, there is a an extra 3 in the 23 square. So this should be a hint to try 239 as a triple, and behold, yes it works. 23,39,29 are all 2 digit subsets of 239. So thus it is a proper triple. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
So when you go to wipe out the 2's, 3's and 9's from the other squares, we end up with the same result as we did when we knew all three. Cool?
Again, the reason this works is because the 239 triple means that those 3 digits will swap amongst those three squares only. We don't know where but they MUST only be there. So to say squares 5,6,9 in our example has an equal chance for all three squares to have the digit 2 still doesn't change the fact that all the other squares in the row are unaffected by this. Reason being of course, the other 6 squares in the row CANNOT have a 2,3, or 9. So in a sense, these three squares can play musical chairs all it wants, because nothing will happen outside of these three squares. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ok, armed with this knowledge, I think most Thursday and even a Friday puzzle is solvable. You should be able to finish most 4 star and even a 5 star puzzles by this point. However, I have run across a few which even with that I am stuck. Is there more? Of course.... | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples
paired sets |
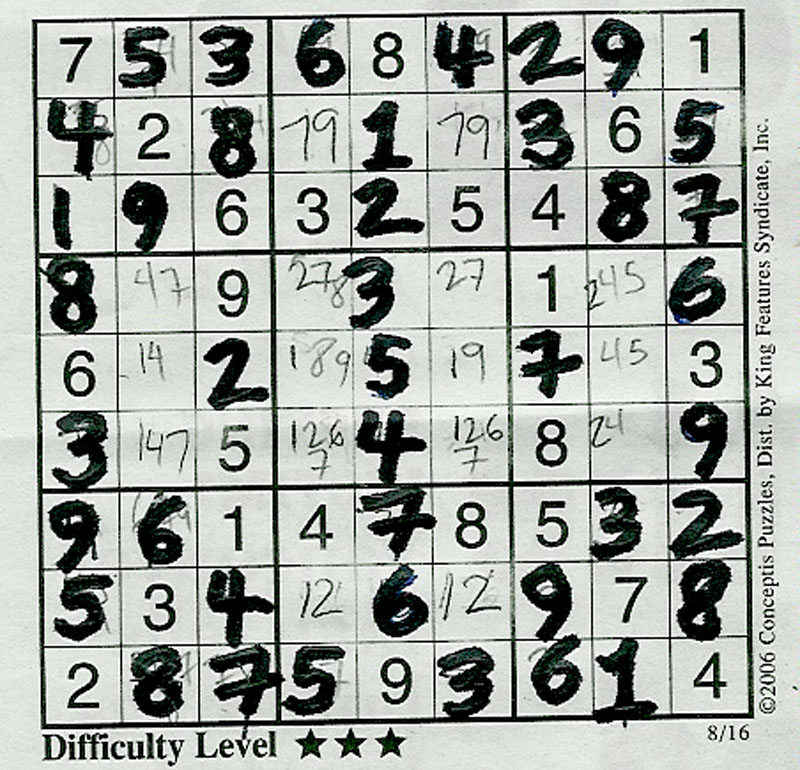
This is from the Vancouver Province 8/16/2006. This isn't the best example I could find but it will do for some illustrations. I have completed the puzzle this far entirely using what we learned in Part 1. You can see by the pencil marks, that by the process of elimination we see many obvious pairs like the 79 pair in row 2, and the 12 pair in row 8. You will also see obvious triples like 147 in column 2 and 245 in column 8. I will direct your attention to row 4: 47, 27, 27, 245. Ok we note that 27 is the pair that MUST be in those two squares in the middle. With that, we can eliminate and simplify the row to 4, 27, 27, 45, alas we solve the row down to 27,27 since the 4 will reduce the 4,5 down to 5. With this, the chain reactions should solve the rest of the puzzle. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples
subset triples set |
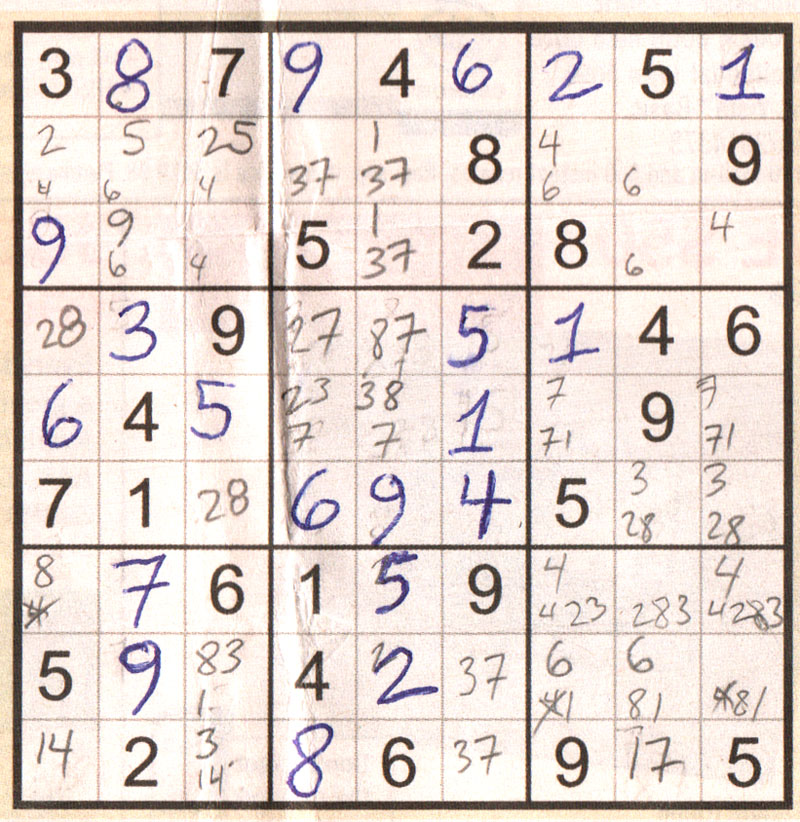
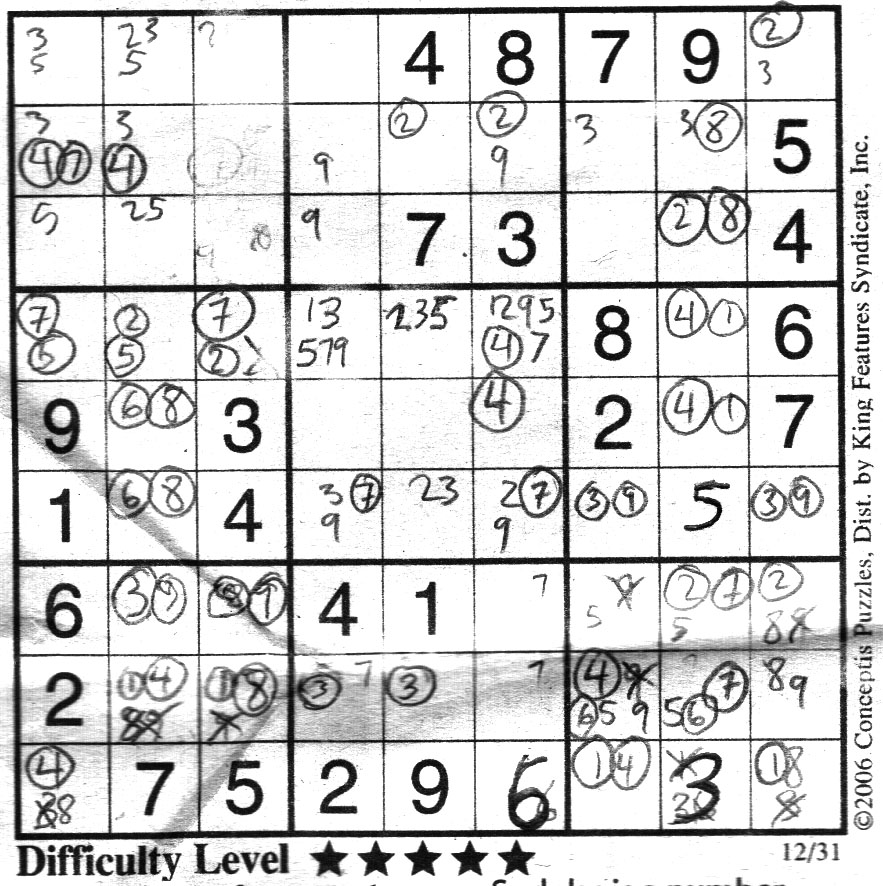 OK, in this puzzle from the Province (12/31/2006). I will draw your attention to block 4 row 4 where there is 57, 25, 27. You should be able spot that as a subset triple of 2,5,7. That will mean you can eliminate all the 2,5, and 7's off that row. That means in block 5: 13579 reduces to 1,3,9 ; 235 reduces to 3 ; 1,2,4,5,7,9 reduces to 1,4,9. This should start the necessary chain reaction needed to finish this puzzle. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples
extending a paired set |
Now you can see that this puzzle is pretty much done. Now if I pencil some of the possible candidates.
What I want to draw you attention to are blocks 4 and 5 and 6. Note that block 5 has a paired set of 1's and 7's. You will also see block 4 has a triple 127, 17 and 12. Now, you will remember that any two candidates within two cells will make a paired set. So, I will draw your attention to row 5. Note that it has 17, 17, 12. The two 17's will make a paired set which means you can eliminate the 1's and 7's from the 12 in block 6, thus simplifying that to a 2. I will pen the 2 in green like follows:
This will of course start a chain reaction of events which should easily solve the rest of the puzzle. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples
row elimination using paired sets |
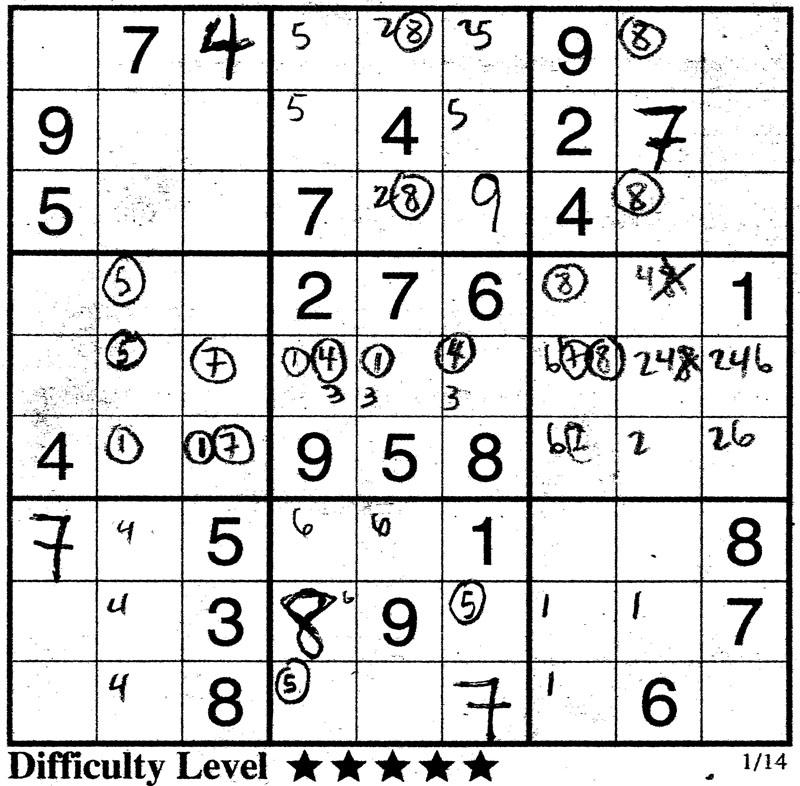
Ok, I take this example from the Vancouver Sun 1/14/2007. Now, I have penciled in some of the possible candidates but I want to draw your attention to the 8's in block 2 and 3. Note that because of the 8's in block 5 and 8, we can only have the 8 in cells 2 and 8 of block 2. We also note that the 8 can only be in cells 2 and 8 of block 3 because of the 8 in column 9 and the filled row in column 7. Well, lo and behold. we have set up a pairing of two 8's in rows 1 and 3. It means that and 8 MUST be in row 1 column 5 or 8 AND an 8 MUST be in row 3 column 5 or 8. Thus, the 8 in block 1 MUST be in row 2. Indeed with the 8 in column 3, we lock the 8 in block 1 in cell 5 like so...
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples
application of paired sets and triple sets |
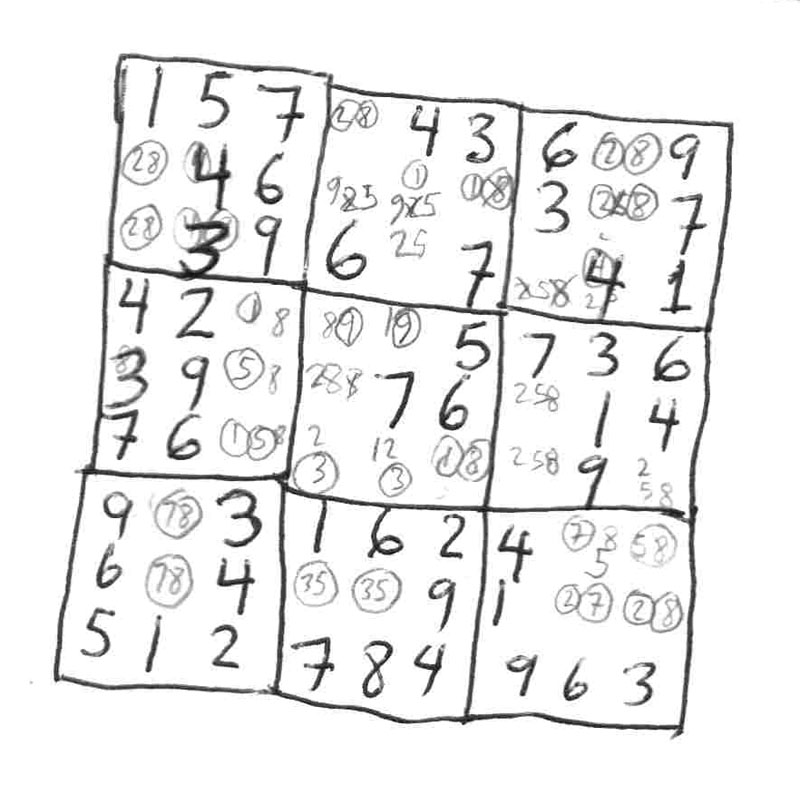
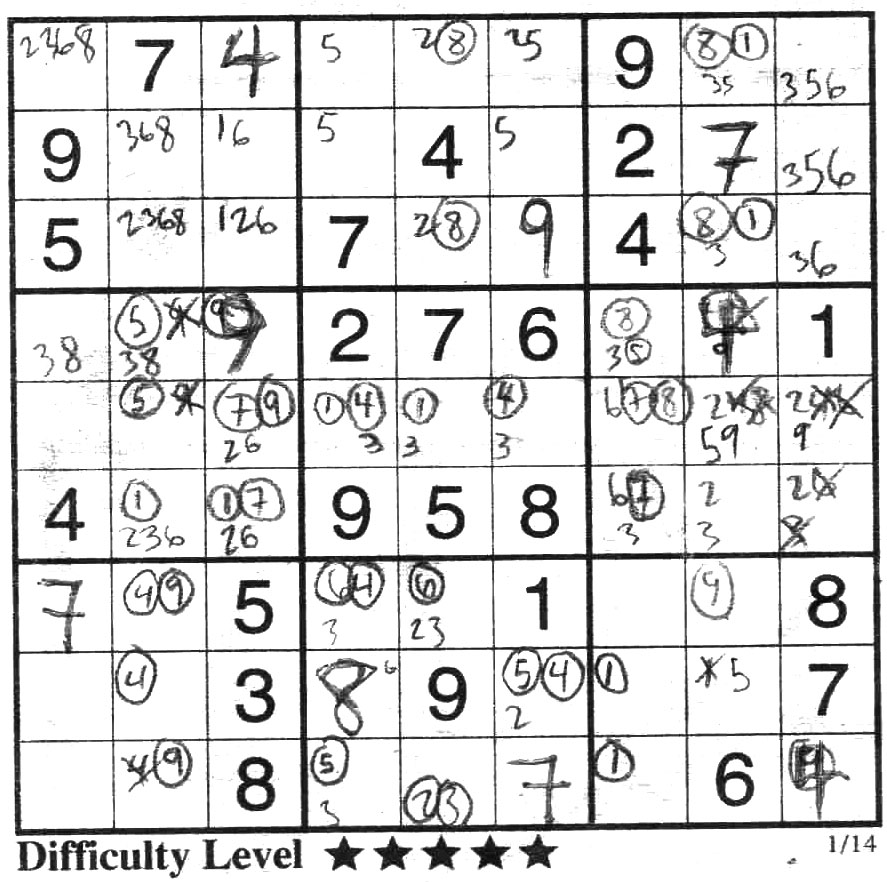 Ok, I continue that puzzle a bit more, and I will now direct your attention to block 3. Due to the 1 and 8 in column 9, we have locked a pair 18 in column 8. Thus we can eliminate the remaining 3 numbers in the remaining 3 squares which are 3,5,6. This is a triple for the column, because this is where 3,5,6 MUST be in this block for this column. This allows you to solve for the 2 and 9 in block 6.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples
application of paired sets and triple sets |
This puzzle from the National Post (rated Diabolical) is not to difficult to get to this point. However, at this point we will have to use something a little more extra punch to get it past this. I draw your attention to column 5. We have 5 squares with 5 candiates left, 1,3,5,7, and 8. The candidate sets are 57,178,1378,358,78. You can probably spot the two 178's right away and there is a lone 78 by itself which is a subset of 178. So we do a split at 178 and 35. Doing the reduction we end up with 5,178,178,35,78. Of course the 5 then reduces the 35 to a 3.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples
application of paired sets and triple sets |
Continuing with the chain reactions caused by the previous example will yield this result:
Now I will direct your attention to block 6. Again, we have 5 blocks with 5 candidate sets, 458,468, 457, 57, and 467. Ok, so how do we split this one? Well, we see a 57 and a 457 which are subset of each other and you really can't break down the other 3. So we will have a 457/68 split. This will reduce our candidate sets down to 8,457,57,47, and 68. The 8 by itself will reduce the 68 down to 6 like follows:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples
paired sets & the box rule |
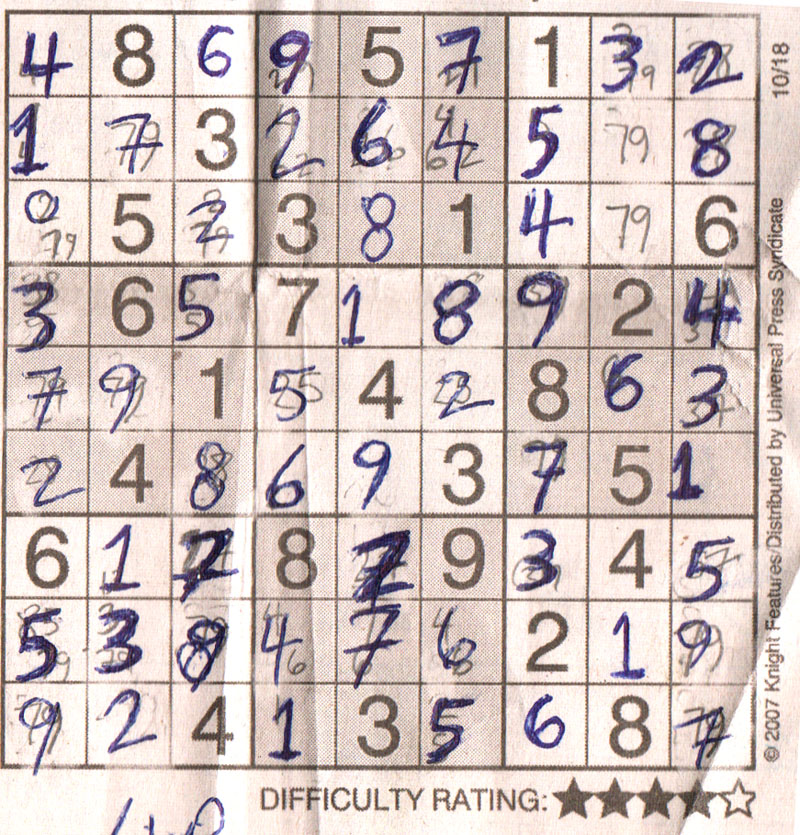
Ok, I will start with row one. It is obvious that 28 is a locked pair since those are the only 2 squares left unsolved and there are only 2 candiates left to solve for them. You can see by column 1 there is also a locked pair of 28. Now you can look at block 3, where you have 28, 258 and 258. Well it is oobvious one the 258 is part of the locked pair 28 but which one. You will lock the centre 258 because it will lock the 28 in row 2 and lock the 28 in column 8. This means the other 258 becomes 5. Also as a note, in column 4 row 2, it has 925, this cell can NOT be 28 because of the unsolved square rule of locked pairs. Thus you can cross off the 2 and from the candidate list for this cell. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples
paired sets & the box rule |
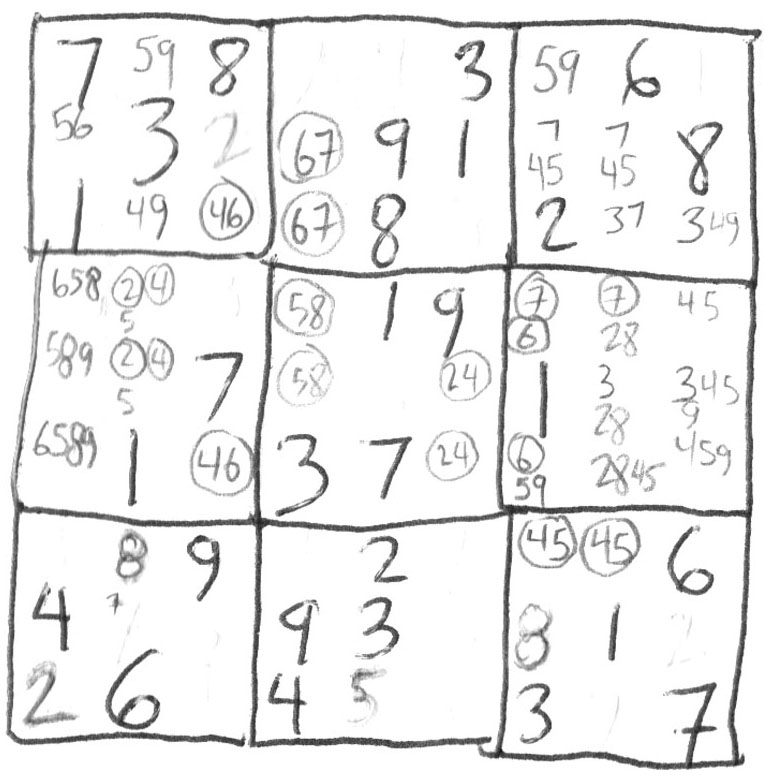 I will direct your attention to column 2. You have 459, 495, 245, 245, 75. You will note the 2's are already locked in place because the two's that were solved in blocks 1 and 7. 9 is also locked in block 1 by the two 9's in block 7 and block 2. You can solve for the 7 in block 7. So that will leave you with 459, 459, 245, 245. 5 was the free floating number since it was 75 in block 7 before you solved it, so the 5 is the extra in the 24 pair just as 4 is the extra in the 59 pair. (This is an extension of the 2/3 combo rule in the next chapter 24/579). This will reduce the two pairs to 59, 9 , 24, 24. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples |
 This puzzle can be solved with just the elimination and pairs rules that you have learned so far. Be careful to keep the candidate lists updated and look for the paired sets. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Examples |
Here are a series of "normal" puzzles. These may seem hard but it doesn't require anything more than process of elimination. Just carefully do your row, column and block candidates and these puzzles will snap together. |
Written by William Chow